Kisi-kisi indikator butir soal dan Butir soal (sesuai dengan kisi-kisi indikator butir soal dari MGMP) disusun dan ditelaah oleh Musyawarah Guru Mata Pelajaran (MGMP) dan dikoordinasikan oleh Dinas Pendidikan Provinsi sesuai dengan kewenangannya kemudian MGMP merakit soal yang disusun oleh guru-guru dari Musyawarah Guru Mata Pelajaran (MGMP) yang telah ditelaah oleh MGMP provinsi dikoordinasikan oleh Dinas Pendidikan Provinsi sesuai dengan kewenangannya yang ditentukan untuk masing-masing mata pelajaran;
Naskah/master soal EHB-BKS beserta kelengkapannya yang disiapkan meliputi naskah soal EHB-BKS Utama dan susulan.
Berikut Soal Latihan dan Pembahasan EHB - BKS MATEMATIKA WAJIB Tahun Pelajaran 2020 - 2021 yang di susun oleh Tim Musyawarah Guru Mata Pelajaran (MGMP) MATEMATIKA SMA Negeri/ Swasta provinsi Jawa Timur berdasarkan pada KISI - KISI EHB - BKS MATEMATIKA WAJIB untuk Refrensi Guru dan Siswa SMA Se-Jatim.
TAHUN PELAJARAN 2020 – 2021
MGMP MATEMATIKA SMA PROVINSI JATIM
KECELAKAAN PESAWAT SRIWIJAYA AIR
Pesawat Sriwijaya Air mengalami kecelakaan dan jatuh di perairan Kepulauan Seribu, untuk menemukan puing-puing pesawat dan juga korban, Tim SAR dan para penyelam melakukan pencarian korban. Setelah beberapa hari dilakukan pencarian ditemukanlah beberapa korban yaitu A, B, C, D, dan E dengan jarak yang selalu bernilai positif atau disebut nilai mutlak. Jarak korban dengan permukaan air laut dituliskan dalam nilai mutlak seperti |A-2|=3 artinya jarak korban A yang bergeser ke kiri 2 meter dari posisi semula dengan permukaan air laut adalah 3 meter. Contoh lain, |3B+1|<6 artinya jarak 3 kalinya korban B bergeser ke kanan 1 meter dari posisi semula dengan permukaan air laut kurang dari 6 meter.
Gunakan teks di atas untuk no. 1, 2, dan 3
1. Jika |2x-1|=5 maka nilai x yang memenuhi adalah…
A. – 6 atau 4
B. – 3 atau 2
C. – 6 atau 4
D. – 4 atau 6
E. 3 atau 2
2. Sesuaikah pernyataan-pernyataan di bawah ini dengan memberi tanda centang
pada kolom yang sudah disediakan.
- Penyelesaian |4x + 2| ≥ 6 adalah x ≤ -2 atau x ≥ 1
- Solusi dari |2x – 1| = |x + 4| adalah x = - 5 ataupun x = 1
- Penyelesaian dari |2x – 1| < 7 adalah -3 < x <
MEMBELI BUKU
Tiga sahabat bernama Ani, Budi, dan Cica sedang pergi ke toko buku untuk membeli buku “Kumpulan soal masuk Perguruan Tinggi” mereka saling berbagi untuk membeli buku-buku tersebut. Ani membeli yang soal TPA, Budi membeli soal Saintek, dan Cica membeli yang soal-soal Soshum. Akhirnya selama berjam-jam mereka mencarinya, buku-buku berhasil mereka peroleh dengan gembira. Mereka berharap dengan buku-buku tersebut dapat belajar dan lolos dalam ujian masuk perguruan tinggi.
Gunakan teks di atas untuk soal no. 4, 5, 6, dan 7
4. Uang Ani Rp.30.000,00 lebih banyak dari uang Budi ditambah dua kali uang
Cica. Jumlah uang Ani,Budi, dan Cica adalah Rp.200.000,00. Selisih uang Budi dan
Cica adalah Rp.5.000,00. Sistem persamaan tiga variabel yang sesuai dengan
pernyataan di atas adalah ….
A. A + B + 2C = 30.000 ; A + B + C = 200.000 ; B – C = 5.000
B. A = B + 2C + 30.000 ; A + B + C = 200.000 ; B – C = 5.000
C. A = B - 2C + 30.000 ; A + B - C = 200.000 ; B + C = 5.000
D. A = B + 2C - 30.000 ; A - B + C = 200.000 ; B – C = 5.000
E. A = - B + 2C + 30.000 ; A + B + C = 200.000 ; B + C = 5.000
PEMBAHASAN:
A = B + 2C + 30.000 ...... (1)
A + B + C = 200.000 ...... (2)
B – C = 5.000 ....... (3)
Dari (1) dan (2) dengan mengeliminasi A diperoleh: 2B + 3C = 170.000 ...... (4)
Dari (3) dan (4) diperoleh: 2B + 3C = 170.000
2B – 2C = 30.000 _
5C = 140.000
C = 28.000
B = 33.000
Substitusi ke (1) diperoleh: A = 33.000 + 56.000 + 30.000 = 119.000
JAWABANNYA B
5. Berdasarkan wacana diatas dan nomor 4, pasangkan untuk setiap anak dan uang
yang dimilikinya agar menjadi benar!
PEMBAHASAN:
A = B + 2C + 30.000 ...... (1)
A + B + C = 200.000 ...... (2)
B – C = 5.000 ....... (3)
Dari (1) dan (2) dengan mengeliminasi A diperoleh: 2B + 3C = 170.000 ...... (4)
Dari (3) dan (4) diperoleh: 2B + 3C = 170.000
2B – 2C = 30.000 _
5C = 140.000
C = 28.000
B = 33.000
Substitusi ke (1) diperoleh: A = 33.000 + 56.000 + 30.000 = 119.000
Jadi ANI = Rp 119.000,00
BUDI = Rp 33.000,00
CICA = Rp 28.000,00
6. Berilah tanda centang pada kotak di bawah ini dari pernyataan-pernyataan yang
benar sesuai wacana dan nomor 4 dan 5. Jawaban benar boleh lebih dari 1.
- Selisih uang Cica dan Budi sebesar Rp. 5.000,-
- Jumlah uang Cica dan Budi sebesar Rp. 5.000,-
- Selisih uang Ani dan Cica sebesar Rp. 91.000,-
- Selisih uang Ani dan Budi sebesar Rp. 91.000,-
PEMBAHASAN :
Selisih uang antara Cica dan Budi = Rp 5.000,00
Jumlah uang antara Cica dan Budi = Rp 61.000,00
Selisih uang antara Ani dan Cica = Rp 91.000,00
Selisih uang antara Ani dan Budi = Rp 86.000,00
MENGHEMAT PENGELUARAN
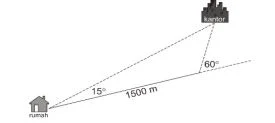
Seorang pegawai ingin menghemat pengeluaran sehingga ia mencari rumah kontrakan yang dekat dengan tempat ia bekerja (kantor) seperti pada gambar.
Untuk memperkirakan jarak dari rumah ke kantor, ia membuat sebuah garis lurus pada jalan sepanjang 1500 m, kemudian ia mengukur sudut yang dibentuk garis tersebut dengan garis (kira–kira) yang menghubungkan titik–titik ujung garis kantor seperti pada gambar.
8. Jarak dari rumah ke kantor adalah ….
- Jarak kantor ke arah sudut 600 menggunakan aturan kosinus dengan sudut apitnya 150
- Jarak rumah ke kantor menggunakan aturan kosinus dengan sudut apit 1200
- Jarak rumah ke kantor menggunakan aturan sinus
- Jarak rumah ke kantor lebih dekat dibanding garis lurus pada jalan sepanjang 1500 m
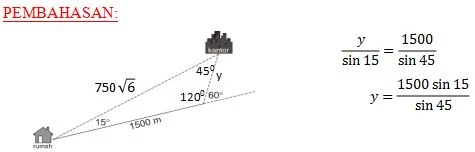
PEMBAHASAN:
1. CENTANG
2. TIDAK CENTANG
3. CENTANG
4. 750V6 = 750 X 2,4 = 1800 > 1500 …….JADI TIDAK CENTANG
10.Jelaskan pendapat kalian dengan memberikan solusi pengerjaan untuk
menentukan unsur-unsur yang belum diketahui dari bangun segitiga
rute perjalanan pegawai kantor tersebut berdasarkan wacana di atas!











Gaada latsol ehb mapel lain?
ReplyDelete